DOS under Windows 98/2000/XP
|
Free C-programs for Unix, Linux and DOS under Windows 98/2000/XP |
|
Back to Stefan's home page
These C-programs are developed by Stefan Spännare and are free to copy.
Read the header of each C-program source code for instructions.
Compiling instructions and
help
for the programs.
1. References
2. Download SSCLN
New!
3. Download SSPROG
Updated!
4. π, Chudnovsky or Ramanujan
5. e=exp(1) and ln(2)
6. Euler C, γ
7. Γ(1/3) and Γ(1/4)
8. Catalan's constant G
9. Apery's constant ζ(3)
10. ζ(s)
11. A program to calculate some mathematical constants to large precision
12. Other e=exp(1) calculating programs
13. Fast hexadecimal e=exp(1) calculating programs
14. Digit statistics
15. Factorial
16. Prime numbers
Updated!
17. Sorting
18. Programs for fun
2. The web page Fast Algorithms and the FEE Method, by Ekatherina A. Karatsuba.
3. The web page The Karatsuba Method 'Divide and Conquer', by Ekatherina A. Karatsuba.
4. The article "Fast evaluation of transcendental functions", Problems of Information Transmission,
vol. 27, (1991), p. 339-360,
by Ekatherina A. Karatsuba.
5. The article "Fast multiprecision evaluation of series of rational numbers", by Bruno Haible and Thomas Papanikolaou, 1997:
6. Some of the programs now use a very fast FFT by Takuya Ooura:
7. The web page CLN - Class Library for Numbers, by Bruno Haible et. al.
8. The documentation "Programs to Calculate some Mathematical Constants to Large Precision", by Stefan Spännare, September 2007:
The short C++ programs in this package use very fast functions in the CLN
(and GMP) packages to calculate some mathematical constants. The results
are interesting in themselves but can also be used to verify calculations
with other programs.
Download:
References:
Important note. According to different references there is a memory limitation
of 32 Mbyte when running programs in DOS (or CMD) mode under Windows
Vista. This makes large calculations with the programs in the NUMBERS directory
impossible under this operating system. How to solve this see the link below.
Windows 7 does probably not have this issue.
Windows Vista restricts non-Win32 apps to 32 MB of memory
All the programs in the package work fine in DOS (or CMD) mode under Windows XP,
2000 and probably also Windows 98.
Important note. The Windows executables compiled with DJGPP under 32-bit
Windows XP DO NOT work on 64-bit Windows operating systems! The author
will investigate the best way how to solve this problem to the next release of
the package. Until then only version 2.26 (with 32-bit executables) is available
for Windows. The author will among other compilers test Microsoft Visual C/C++
Express Studio Edition 2008 which can be downloaded for free here. Hopefully
it can be run in console mode.
Microsoft Visual Studio Express Edition
Note,
the Unix and Linux package now includes cbrun2l32, cbrun2l64, cbrun3l32
and cbrun3l64 executables for Linux (in the PRIMES directory) compiled using
Intel C/C++ 11.1 (icc) with the "-pc80" (long double) option. Versions are
available for both 32-bit and 64-bit Linux. The executables are compiled for
Pentium 3, Pentium 4 and Core 2 Duo processors. Some of them work well
also on AMD CPUs.
Note,
September 20 2010. The next release of the package will involve some updates
of the programs in the in the NUMBERS directory. This update will probably come
during 2011.
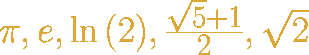
This program uses some (not that fast) AGM based algorithms.
The program uses a very fast FFT (fftsg_h.c)
by Takuya Ooura. Many thanks to him!
Slower floating point method, probably numerically stable:
Long long int (64 bit) integer method, numerically stable:
Chose the program that is fastest on your computer:
The following program is also needed for the final result:
Programs to convert from hexadecimal to decimal:
Why not check if the digits seem to have a normal distribution:
This program calculates large factorials (n!) exactly:
All the prime number programs use a segmented implementation of Eratosthenes sieve.
They are very fast and require very little memory.
These two programs works theoretically for n ≤ 253-1 ≈
9.0·1015.
This program calculates (and print) all primes below n.
This program makes a table of the number of primes and twin primes below n.
These programs calculate Bruns constant and the Twin prime constant and the number
of primes and twin primes below n.
Works theoretically for n ≤ 264-1 ≈
1.8·1019.
(using long double numbers). The programs cbrun2l* and cbrun3l* are significantly
faster than cbrunl for large n (≥ 1010).
Some results from the programs.
Quick sort (very fast, non recursive and recursive):